1.1 Billion

That’s the number of heartbeats in every animal’s lifetime*. Don’t believe me?

Let’s consider an extreme comparison. A mouse can live for 3 years, and has a heartbeat of about 670 beats per minute. There are 525600 minutes in a year (365 days/year * 24 hours/day * 60 minutes/hour). So, that’s 3 years/lifetime *525600 minutes per year * 670 beats/minute ≈ 1.1 billion beats/lifetime. What about an elephant? They can live up to 70 years and have a heartbeat of about 30 beats/minute. 70 years/lifetime * 525600 minutes/year * 30 beats/minute ≈ 1.1 billion beats/lifetime. Woah… what?!

Ok, ok… you probably noticed that those “equals” signs are actually squiggly “approximately” signs, and if you did the math (you should!) you would see that they are both a little off from exactly 1.1 billion. But still, they are damn close. What gives? Why would the number of heartbeats be an invariant property of the animal kingdom? Let’s dive a little deeper.

The answer lies in allometric scaling, or how different properties of life scale with the body mass of organisms. It turns out that the power (energy per time, metabolism) required to support a given unit of mass of an organism scales with the mass of that organism to the (-1/4) power- meaning that smaller organisms use energy at a faster rate per unit mass than larger organisms. Other rates, such as breathing rate and heartbeat rate, also scale with bodymass^(-1/4). Lifespan, on the other hand, has been shown to scale with bodymass^(1/4). If you want to find how the lifetime total beats scale, you can multiply those two together (beats/time * time = beats). Bodymass^(-1/4) * Bodymass^(1/4) = Bodymass^0, which is always 1, meaning that the total beats is invariant of bodymass! More on allometry and metabolism in later posts. And maybe I’ll learn how to show equations in wordpress someday.

This paper (which probably takes into account more than the 2 points I used above) cites the total number of heartbeats in an animals lifetime as 1.5 billion.

Now, given this number, can we backtrack and use the relationship to see how long humans are predicted to live? Given a certain heart-rate, how long would it take us to use up our 1.5 billion?

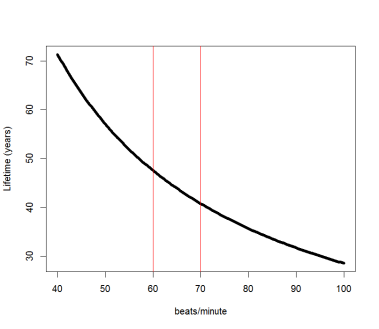
R code:
curve(1.5e9/(x*525600), xlim=c(40,100), lwd=5,
ylab=”Lifetime (years)”, xlab=”beats/minute”);
abline(v=60, col=”red”);abline(v=70, col=”red”)

If an animal beats its heart between 60 and 70 times a minute, it would use up its 1.5 billion beats in around 40-45 years. Is this a ballpark estimate of a human’s lifetime in the wild? (Aside: if you take the 1.1 billion heart beats derived from mice and elephants and assume a heart-rate of 70 beats per minute for humans you get 29.9 years!)

Now, don’t worry. Humans have found amazing ways to increase their lifespan, and it’s not like everyone has a set number of heart beats to get through before it’s all over. This is just an interesting result of looking at metabolism and ecology – and what’s even more interesting is looking at the animals that stray from the predictions.

*That’s about the predicted number of heartbeats in an average organism’s lifetime